Microscopic modeling of compact stars
Since the recent (2017) detection of gravitational waves (GW) during the coalescence of two neutron stars (NS) leading to the emergence of multi-messenger astronomy, it is clear that nuclear physics has a key role to play in the understanding of these spectacular astrophysical phenomena, by providing microscopic theoretical and experimental data that can be directly connected with the observations.
The LPC theory team has been involved for several years in the microscopic modeling of dense matter as found in all astrophysical phenomena concerning compact stars, namely neutron stars and proto-neutron stars (pulsars, magnetars, gamma and X-ray sources), core-collapse supernovae and neutron star binaries, with various theoretical methods (variational approaches, extended Thomas-Fermi theory, relativistic mean-field, compressible liquid droplet model, statistical models). More specifically, our expertise concerns the theoretical modeling of the equation of state (EoS), composition and phase transitions of baryonic matter under conditions of density and temperature where it can be described by nucleonic or hyperonic degrees of freedom. In the context of the current discoveries, our research aims (i) on the one hand to establish a direct and quantitative connection between microphysical data and astrophysical observables using advanced statistical techniques, (ii) and on the other hand to develop original theoretical tools to describe the EoS at finite temperature, a subject that is still treated with strong approximations.
Degenerate regime
We have developed an EoS meta-modeling technique [3] that allows to extrapolate with Bayesian techniques the uncertainties on microscopic data (experimental or theoretical) into controlled predictions of astrophysical observables, such as masses and radii of compact stars, tidal polarizability measurable by the GW signal, moment of inertia of the crust, amplitude of pulsar glitches.
We have extended the formalism initially valid only for homogeneous matter in the liquid phase, to the solid phase of the crust and the associated inhomogeneous matter [7]. This allowed us to have a unified treatment of the EoS which we showed to be essential for a correct evaluation of the NS radius [1] as can be estimated by tidal polarizability measurements, and to show for the first time the key role of the surface energy of very neutron-rich nuclei in the determination of the crustal properties.
Figure tirée de DOI: 10.1103/PhysRevC.100.055803
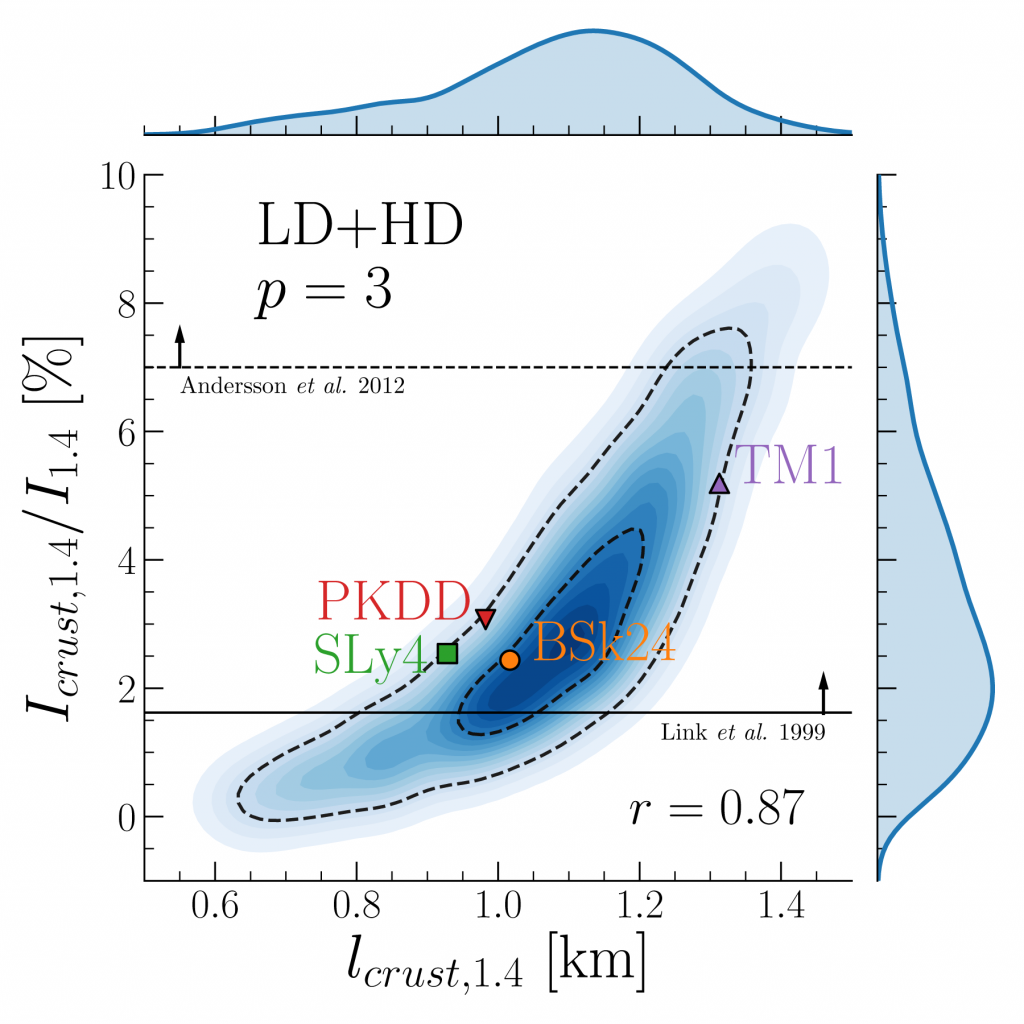
Bayesian estimation of the moment of inertia (ordinate) and thickness (abscissa) of a neutron star of mass M=1.4Mo, taking into account constraints from experimental nuclear physics data, ab-initio calculations, and observational constraints. The symbols give the predictions of some popular equation of state models.
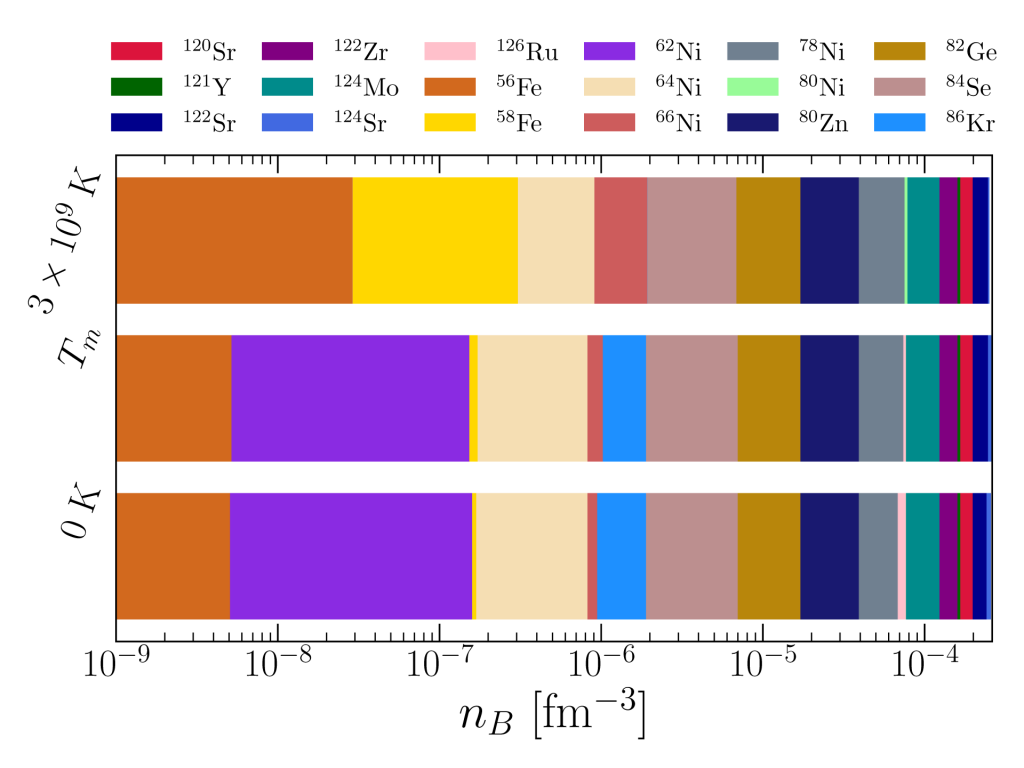
Composition of the crust of a neutron star at different temperatures, where Tm is the crystallization temperature, obtained with the BSK24 unified equation of state.
Figure tirée de http://www.theses.fr/2020NORMC206
The obvious continuation of this project concerns the proposal of waveforms for the analysis of GW signals incorporating the current microscopic knowledge of the EoS. For this purpose, the team is part of the VIRGO/LIGO collaboration since December 2020.
Finite temperature
The additional difficulty of finite temperature modeling is that, if the density is below the nuclear saturation density, the matter is organized into clusters of nucleons and the statistical distribution of microstates must be explicitly considered. We have produced [5] the only equation-of-state table including the complete cluster distributions and based on modern non-relativistic functionals that is publicly available for direct use in core collapse calculations. This table is available on the CompOse archive and partially allows to test the effect of microphysics on the collapse, by comparison with relativistic models computed by other teams and available on the same archive.
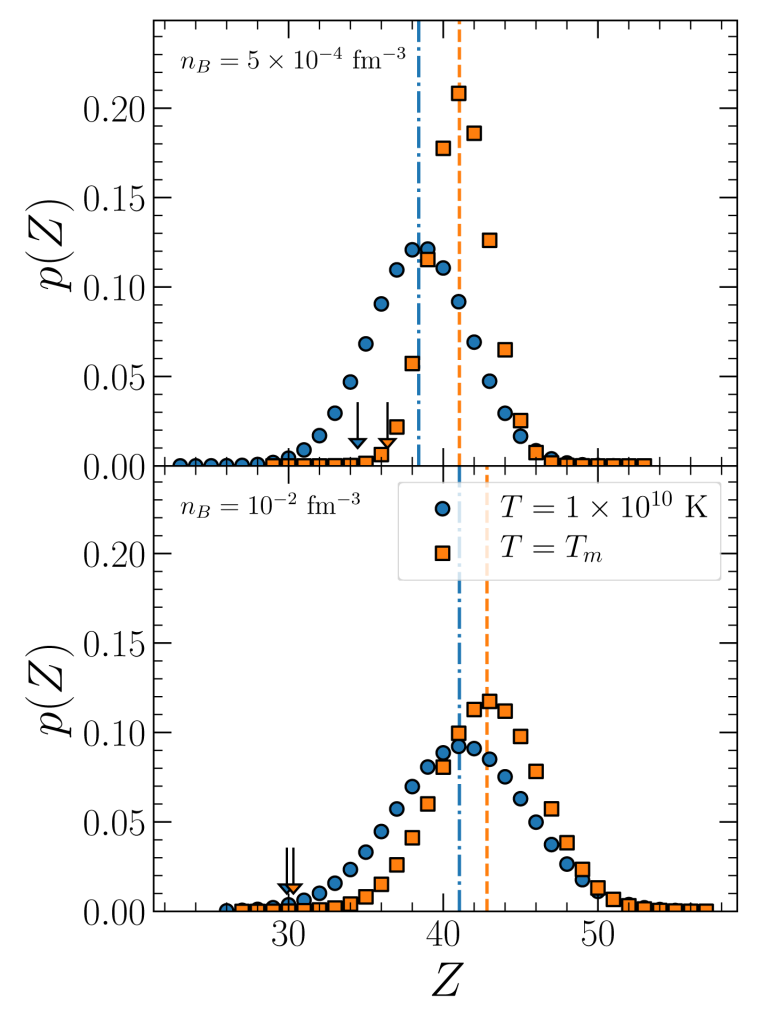
In order to be able to test separately the different physical ingredients, we have developed [4] an original perturbative theoretical approach that allows to compute the cluster distribution from any standard EoS model, based on the single nucleus approximation. Thanks to this approach, we have been able to deconvolute the effect of the different ingredients, and to show that the key variable is given by the electron capture rates on very neutron rich nuclei [2]. Very recently [8], we have extended this approach to the study of crustal crystallization and produced the first self-consistent microscopic calculation of the impurity factor that governs the neutrino scattering rates in proto-NS.
Figure tirée de : https://doi.org/10.1051/0004-6361/202038347
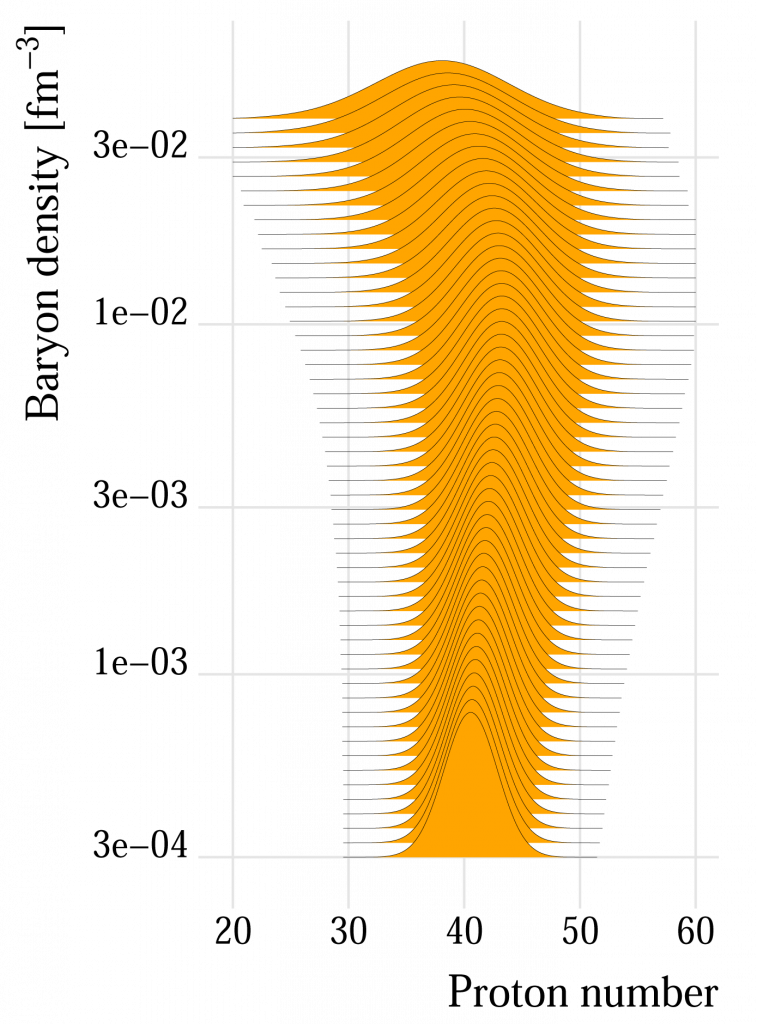
Distribution of nuclei at different densities and temperatures. The simplified estimate of the single nucleus approximation is given by the vertical lines.
Finally we started to tackle the problem of determining the mass change of light clusters in a dense medium [6] and suggested a novel method of analyzing nuclear multi-fragmentation data to be able to constrain the parameters of the theory.
Figure tirée de : https://doi.org/10.1051/0004-6361/202038347
Read more
-
1. M. Fortin, C. Providência, Ad. R. Raduta, F. Gulminelli, J. L. Zdunik, P. Haensel, and M. Bejger “Neutron star radii and crusts: Uncertainties and unified equations of state”, Phys. Rev. C 94, (2016) 0358041. M. Fortin, C. Providência, Ad. R. Raduta, F. Gulminelli, J. L. Zdunik, P. Haensel, and M. Bejger “Neutron star radii and crusts: Uncertainties and unified equations of state”, Phys. Rev. C 94, (2016) 035804
-
2. Ad. R. Raduta, F. Gulminelli, M. Oertel, “Stellar electron capture rates on neutron-rich nuclei and their impact on core-collapse” PHYSICAL REVIEW C 95 (2017) 025805 (ArXiV:161101744)2. Ad. R. Raduta, F. Gulminelli, M. Oertel, “Stellar electron capture rates on neutron-rich nuclei and their impact on core-collapse” PHYSICAL REVIEW C 95 (2017) 025805 (ArXiV:161101744)
-
3. J. Margueron, R.H.Casali, F. Gulminelli “The equation of state for dense nucleonic matter from metamodeling:I. foundational aspects”, Phys.Rev. C97(2018)025805 (ArXiv:1709.00189)3. J. Margueron, R.H.Casali, F. Gulminelli “The equation of state for dense nucleonic matter from metamodeling:I. foundational aspects”, Phys.Rev. C97(2018)025805 (ArXiv:1709.00189)
-
4. G.Grams, S.Giraud, A.Fantina and F.Gulminelli, « Nuclear distribution from a free energy density in a Wigner-Seitz Cell », Phys. Rev. C 97 (2018) 0358074. G.Grams, S.Giraud, A.Fantina and F.Gulminelli, « Nuclear distribution from a free energy density in a Wigner-Seitz Cell », Phys. Rev. C 97 (2018) 035807
-
5. Ad.A.Raduta and F.Gulminelli, “Nuclear Statistical Equilibrium equation of state for core collapse”, Nuclear Physics A 983 (2019) 2525. Ad.A.Raduta and F.Gulminelli, “Nuclear Statistical Equilibrium equation of state for core collapse”, Nuclear Physics A 983 (2019) 252
-
6. H.Pais, F.Gulminelli, C.Providencia, and G.Roepke, “Light clusters in warm stellar matter: explicit mass shifts and universal cluster-meson couplings”, Physical Review C 97, 045805 (2018)6. H.Pais, F.Gulminelli, C.Providencia, and G.Roepke, “Light clusters in warm stellar matter: explicit mass shifts and universal cluster-meson couplings”, Physical Review C 97, 045805 (2018)
-
7. T.Carreau, F.Gulminelli, J.Margueron, « General predictions for the neutron star crustal moment of inertia», PRC (2019)7. T.Carreau, F.Gulminelli, J.Margueron, « General predictions for the neutron star crustal moment of inertia», PRC (2019)
-
8. A.Fantina, S.de Ridder, N.Chamel, F.Gulminelli, “Crystallization of the outer crust of a non-accreting neutron star”, A&A (2019)8. A.Fantina, S.de Ridder, N.Chamel, F.Gulminelli, “Crystallization of the outer crust of a non-accreting neutron star”, A&A (2019)