Physics of ultra-cold atoms
Atomic gases trapped in optical lattices allow a quasi-perfect realization of the Hamiltonians used in condensed matter physics. In this context, a major challenge lies in the understanding of the low energy properties of the Hubbard model in two dimensions because of its possible connections with the high critical temperature of superconductivity in cuprates. The work carried out at the LPC has pursued the objective of a determination of the ground state of this model as a function of site interaction and density. We have extended an approach commonly used in nuclear structure where correlations are introduced through the restoration of deliberately broken symmetries in a test state in the form of a superposition of Hartree-Fock-Bogoliubov (HFB) wave functions. No magnetic, charge or superfluid order is assumed in this state which is optimized to minimize the energy after projection onto the relevant quantum numbers. Through numerical simulations on large rectangular hole-doped cells, an intertwining of spin, charge and d-wave pair degrees of freedom has been demonstrated. At strong coupling, it has been shown [9] that the associated correlations develop cooperatively and are in general spatially modulated. Around the 1/8 doping, such an entanglement is interpreted in terms of vertical charge ribbons separating antiferromagnetic domains and supporting a d-wave Cooper pair condensation in the zero momentum channel as well as in the charge density wave vector channel [9]. This inhomogeneous superfluidity is thus similar to a realization of the Fulde-Ferrell-Larkin-Ovchinnikov phase, but with an order parameter possessing d symmetry.
A new quantum Monte Carlo (QMC) method has also been proposed to achieve a more accurate description of the strongly correlated superfluid phases exhibited by the ultra-cold Fermi gases. While traditional QMC reformulations of the fermionic N-body problem are based on Slater determinants, we have shown that it is also possible to reconstruct the ground state through HFB wavefunctions following a Brownian in imaginary time guided by a trial state. This is also used to constrain the stochastic realizations and thus control the traditional phase problems that usually contaminate QMC sampling for interacting fermions. Encouraging exploratory results have been obtained for the Hubbard model in the attractive and spin polarized regime.
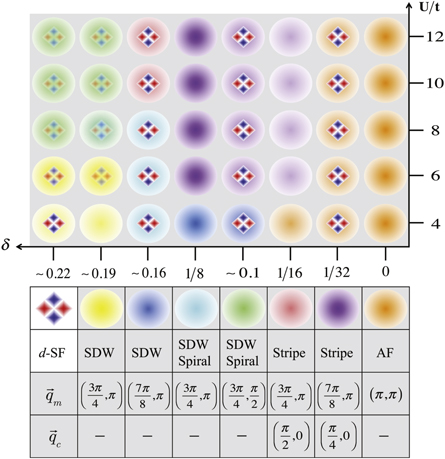
Phase diagram resulting from the HF/BdG projected symmetry approach for repulsively interacting cold fermions in optical tubes. The colours refer to the different magnetic (charge) orders, revealed by a peak in the Fourier transform of the spin (density) autocorrelation function.
Read more
-
A. Leprévost, O. Juillet and R. Frésard, « Intertwined orders from symmetry projected wavefunctions of repulsively interacting Fermi gases in optical lattices », New Journal of Physics 17, 119501 (2015).A. Leprévost, O. Juillet and R. Frésard, « Intertwined orders from symmetry projected wavefunctions of repulsively interacting Fermi gases in optical lattices », New Journal of Physics 17, 119501 (2015).