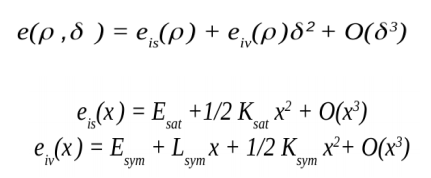Nuclear physics

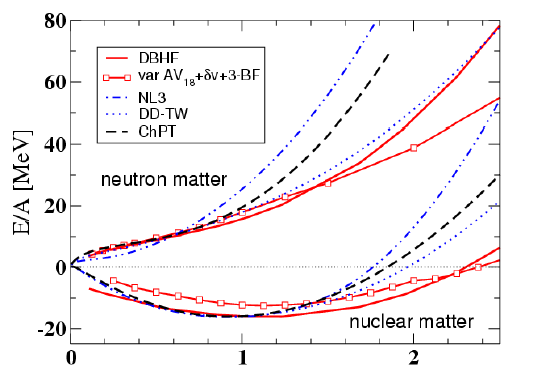
The equation of state determines the response of atomic nuclei subjected to external excitations such as those encountered during collisions between nuclei (pressure and temperature), as well as that of nuclear matter during the collapse phase of type II supernovae (so-called core-collapse supernovae). The equation of state is a mathematical relationship that links thermodynamic quantities such as energy, temperature, pressure, density, and isospin defined as the ratio between the number of neutrons N and protons Z of nuclear matter. Nuclear matter is defined as the thermodynamic limit of a Fermi fluid characterized by a large number of protons and neutrons as found in compact stars (neutron stars). At zero temperature, we approximate the energy e(ρ,δ) of the system characterized by the density ρ=ρn+ρp and the isospin δ=(ρn-ρp)/ρ where ρn and ρp are respectively the densities of neutrons and protons by 2 terms eis and eiv. The first eis is the isocalar term which depends only on the total density ρ=ρn+ρp, while the second is the isovector term which depends on the difference ρn-ρp. The expansion here is stopped at order 2 in δ because for ordinary nuclear matter we have : δ<<1. We speak of symmetric nuclear matter when δ=0 either ρn=ρp. The expansion here involves only even terms in δ because of isospin symmetry which states that e(ρ,δ)=e(ρ,-δ). The eis and eiv terms are also described via a density-limited expansion by the quantity x=(ρ+ρ0)/3ρ0 where ρ0 is here the saturation density of nuclear matter which is ρ0≈ 0.16 fm-3. The different terms of these developments give the coefficients of the equation of state called Ksat (incompressibility modulus) at order 2, Esym (symmetry energy at ρ=ρ0) at order 0, Lsym (slope of the symmetry energy) at order 1, Ksym (curvature) at order 2 as shown in the equations below.